이진탐색트리(Binary Search Tree)

얼마 전, 스타트업 면접에서 이진탐색트리인지 확인하는 함수를 작성하라는 질문을 받았었습니다. 입력으로 들어오는 Node 클래스도 제가 정의해서 구현했어야 했는데, 부모를 가리키는 parent 멤버변수를 Node 클래스에 넣지 않아 한참을 해맸었습니다. 면접을 마치고 아쉬움이 많이 남아 BST에 대해 완벽하게 이해하고자 이 글을 작성했습니다.

이진탐색트리(Binary Search Tree)란?

이진탐색트리는 왼쪽 서브트리는 자기자신보다 모두 작고, 오른쪽 서브트리는 자기자신보다 모두 큰 특성을 유지하는 트리입니다.

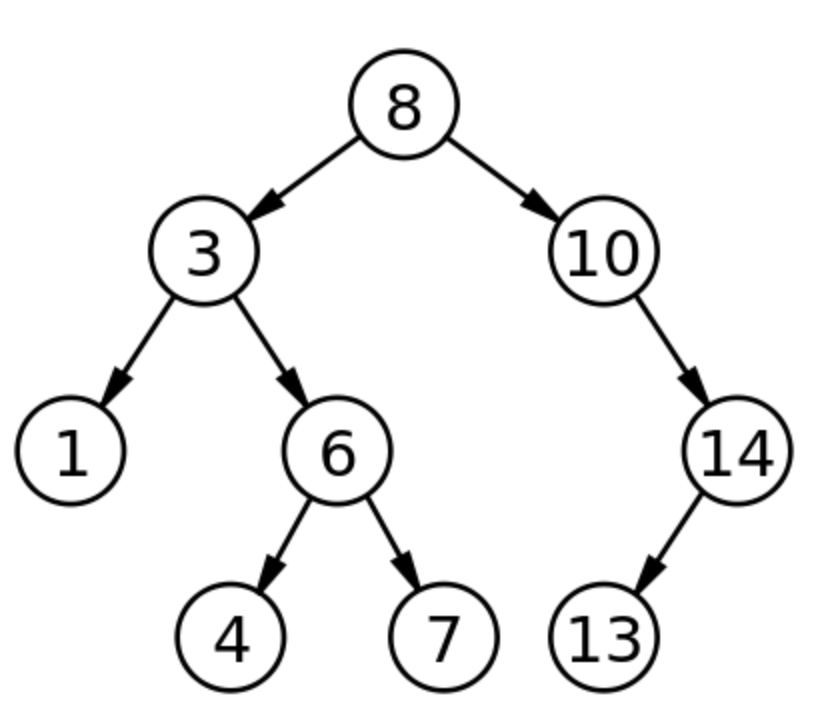
이진탐색트리(Binary Search Tree)는 이진탐색(Binary Search)과 연결리스트(LinkedList)를 결합한 자료구조입니다. 이진탐색트리는 이진탐색의 효율적인 탐색능력과, 연결리스트의 장점을 모두 따와 노드의 탐색과, 삽입, 삭제연산에 대해 평균적으로 O(logN)의 시간복잡도를 보입니다. 이진탐색트리는 다음 네 가지 특성을 가집니다.

모든 노드의 키는 유일한 값을 가진다.(중복된 노드 X)
왼쪽 서브트리의 키들은 루트노드의 키보다 작다.
오른쪽 서브트리의 키들은 루트노드의 키보다 크다.
노드의 각 서브트리는 이진탐색트리이다.

시간복잡도

이진탐색트리의 삽입, 삭제, 탐색 연산의 시간복잡도는 트리의 높이에 비례합니다. 따라서 이진탐색트리가 균형잡혀 있다면 O(logN)에 연산을 수행할 수 있지만, 트리가 편향돼 있다면 최악의 경우 O(N)의 시간복잡도를 보일 수 있습니다.

이진탐색 트리가 편향된 경우

두 트리는 모두 이진탐색트리의 조건을 만족합니다. 그러나 트리가 편향되어 있기 때문에, 트리의 높이 h = 노드의 갯수가 됩니다. 이진탐색트리의 삽입, 삭제, 탐색의 성능은 트리의 높이에 비례하기 때문에 이 경우 시간복잡도는 모두 O(h=n)이 되게 됩니다. 이러한 이진탐색트리의 편향 문제를 해결하기 위해 AVL Tree, Red-Black-Tree 등의 자료구조가 등장하게 됩니다.

이진탐색트리의 탐색(Search)

이진탐색트리의 탐색은 간단합니다. 찾고자 하는 값을 현재 노드와 비교해가며 자식노드로 내려가 원하는 값이 있는지 확인합니다. 다음은 이진탐색트리의 탐색과정입니다.

현재 노드의 값과 찾고자 하는 값이 일치하면 현재 노드를 반환합니다.
현재 노드의 값보다 찾고자 하는 값이 크면 오른쪽 자식노드로 이동합니다.
현재 노드의 값보다 찾고자 하는 값이 작으면 왼쪽 자식노드로 이동합니다.
1 ~ 3 을 반복합니다.

이진탐색트리의 search 구현

public Node search(int key){
  Node temp = this.head;
  while(temp != null){
    if(temp.key == key)
      return temp;
    temp = temp.key < key ? temp.right : temp.left;
  }
  return null // 찾고자 하는 값이 트리에 없을 경우 null 반환
}

이진탐색트리의 삽입(Insert)

이진탐색트리의 삽입은 탐색과 유사합니다. 다음은 이진탐색트리의 삽입과정입니다.

현재 노드가 null 이면 현재 위치에 노드를 삽입합니다.
현재 노드의 값이 삽입할 값과 일치하면 삽입하지 않고 false를 반환합니다.
현재 노드의 값보다 삽입할 값이 크면 오른쪽 자식노드로 이동합니다.
현재 노드의 값보다 삽입할 값이 작으면 왼쪽 자식노드로 이동합니다.
1 ~ 4 를 반복합니다.

이진탐색트리의 Inseart 구현

public boolean Insert(Node input){
  if(this.head == null){
    this.head = input;
    return true;
  }
  Node temp = head;
  Node parent = temp.parent;

  while(temp != null){
    // 값이 이미 있는 경우 false 반환
    if(input.key == temp.key)
      return false;
    temp = temp.key < input.key ? temp.right : temp.left;
    parent = temp;
  }

  if(parent.key < input.key)
    parent.right = input;
  else
    parent.left = input;

  input.parent = parent;
  return true;
}

이진탐색트리의 삭제(Delete)

이진탐색트리의 삭제는 탐색과 삽입연산보다 까다롭습니다. 삭제할 노드의 자식노드가 없다면 노드를 지우기만 하면 되지만, 자식노드가 있을 경우, 부모노드와 자식노드를 연결해줘야 하기 때문입니다. 이 때 이진탐색트리의 성질을 유지한 채로 연결을 해줘야 합니다.

이미지 출처: http://www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/9-BinTree/BST-delete2.html

이 때 연결을 맡을, 다시 말해 삭제할 노드를 대체할 노드는 삭제할 노드의 왼쪽 노드 중 가장 큰 노드, 혹은 삭제할 노드의 오른쪽 노드 중 가장 작은 노드를 선택합니다. 왼쪽 서브트리 중 가장 큰 노드는 모든 왼쪽 노드 중 가장 크며, 삭제할 노드의 오른쪽 서브트리의 모든 노드보다는 작기 때문에 삭제할 노드를 대체할 수 있기 때문입니다. 오른쪽 서브트리 중 가장 작은 노드도 이와 동일합니다.

다음은 이진탐색트리의 삭제과정입니다.

삭제할 값을 가진 노드를 찾습니다.
삭제할 노드가 존재하지 않으면 false를 반환합니다.
삭제할 노드가 단말노드라면 삭제하고 true를 반환합니다.
한쪽 서브트리만 존재할 경우, 삭제할 노드의 자식노드와 부모노드를 연결하고 true를 반환합니다.
양쪽 서브트리가 모두 존재한다면, 삭제할 노드를 대체할 노드를 찾아 서브트리와 부모노드를 연결합니다.

이진탐색트리의 Delete 구현

public boolean delete(int element){
  Node target = search(element);

  if(target == null)
    return false;

  if(target.left == null && target.right == null){
    target = null;
    return true;
  }

  // 오른쪽 서브트리만 존재할 때
  if(target.left == null){
    if(target.parent.left == target)
      target.parent.left = target.right;

    if(target.parent.right == target)
      target.parent.right = target.right;

    target.right.parent = target.parent;
    return true;
  }
  // 왼쪽 서브트리만 존재할 때
  if(target.right == null){
    if(target.parent.left == target)
      target.parent.left = target.left;
    if(target.parent.right == target)
      target.parent.right = target.left;

    target.left.parent = target.parent;
    return true;
  }
  // 양쪽 서브트리 모두 존재할 때
  else{
    Node alternativeNode = findMinNode(target.right);    // 오른쪽 서브트리에서 가장 작은 값을 찾음.
    if(alternativeNode == target.right)
      target.right = null;
    else
      alternativeNode.parent.left = null;

    alternativeNode.left = target.left;
    if(alternativeNode.left != null)
      alternativeNode.left.parent = alternativeNode;

    alternativeNode.right = target.right;
    if(alternativeNode.right !- null)
      alternativeNode.right.parent = alternativeNode;

    alternativeNode.parent = target.parent;

    if(target.parent.left == target)
      target.parent.left = alternativeNode;
    else if(target.parent.right == target)
      target.parent.right = alternativeNode;

    target = null;
    return true;
  }

  return false;
}

public Node findMinNode(Node target){
  while(target.left != null)
    target = target.left;
  return target;
}

이진탐색트리의 순회

이진탐색트리를 중위순회하면 정렬된 값을 얻을 수 있습니다.

이진탐색트리를 중위순회로 출력하는 함수 구현

public void print(Node temp){
    if(temp == null)
        return;

    print(temp.left);
    System.out.println(temp.element);
    print(temp.right);
}

저작자표시 비영리 변경금지

나의 오늘들

이진탐색트리(Binary Search Tree)

이진탐색트리(Binary Search Tree)